
Measurements of this kind require means to generate and visualize frequency distributions, so-called histograms, and stringent statistical treatment to extract the model parameters from purely statistical distributions. In Quantum mechanics, models typically only predict the probability density function (“pdf”) of measurements depending on a number of parameters, and the aim of the experimental analysis is to extract the parameters from the observed distribution of frequencies at which certain values of the measurement are observed. A usable tool therefore must contain easy-to-use and efficient methods for storing and handling data.
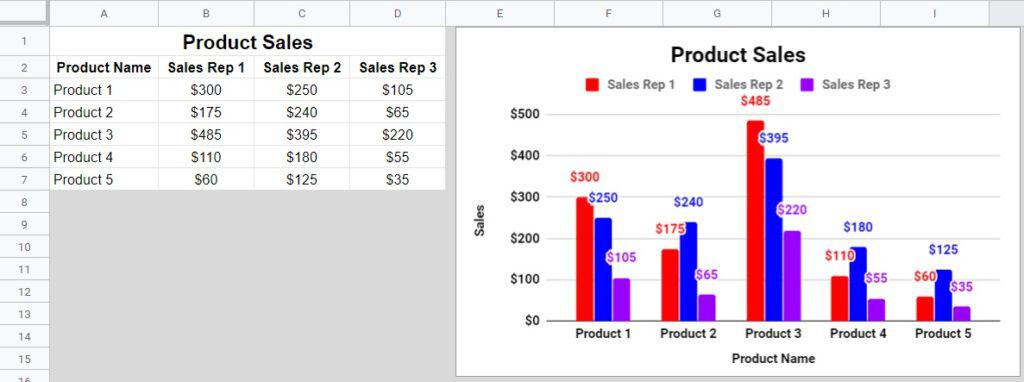
Quite often, the data volume to be analyzed is large - think of fine-granular measurements accumulated with the aid of computers. Means to quantify the level of agreement between measurements and model must also be available. Several standard methods are available, and a data analysis tool should provide easy access to more than one of them. See Figure 1.1 for an example of a function (model) fit to data points.
#Create a graph free#
In subsequent analysis, the statistical nature of the errors must be handled properly.Īs the last step, measurements are compared to models, and free model parameters need to be determined in this process. One specialty of experimental physics are the inevitable uncertainties affecting each measurement, and visualisation tools have to include these. Quite often, these manipulations are complex ones, and a powerful library of mathematical functions and procedures should be provided - think for example of an integral or peak-search or a Fourier transformation applied to an input spectrum to obtain the actual measurement described by the model. Next, some manipulations typically have to be applied, e.g. corrections or parameter transformations. Such a model may simply state “the current I is proportional to the voltage U”, and the task of the experimentalist consists of determining the resistance, R, from a set of measurements.Īs a first step, a visualisation of the data is needed. Very often, the model depends on parameters. In the most simple case, a “model” is just a function providing predictions of measured data.
Zeise 1 Motivation and IntroductionĬomparison of measurements to theoretical models is one of the standard tasks in experimental physics. This introductory guide illustrates the main features of ROOT which are relevant for the typical problems of data analysis: input and plotting of data from measurements and fitting of analytical functions. Among its prominent features are an advanced graphical user interface, ideal for interactive analysis, an interpreter for the C++ programming language, for rapid and efficient prototyping and a persistency mechanism for C++ objects, used also to write every year petabytes of data recorded by the Large Hadron Collider experiments.
#Create a graph software#
ROOT is a software framework for data analysis and I/O: a powerful tool to cope with the demanding tasks typical of state of the art scientific data analysis. A ROOT Guide For Beginners A ROOT Guide For Beginners


 0 kommentar(er)
0 kommentar(er)
